Como parte de la renovación de nuestra instalación eléctrica, se dispone en la explotación de una aeroturbina.
Se pide determinar la energía que produce dicha aeroturbina en 10 horas, sobre la que actúa un viento de 22.22 m/s, si sus palas son de 4 m de radio cada una.
Considerar la densidad del viento 
= 0.928 kg/m3.
Este ejercicio apareción en la prueba práctica del examen de oposiciones a profesor de Tecnología de Extremadura 2025
En nuestra misión por modernizar las explotaciones industriales y hacerlas más sostenibles, la aeroturbina se ha convertido en una pieza clave. Pero, ¿alguna vez te has preguntado cuánta energía puede generar realmente ese «gigante» de metal?
Hoy vamos a resolver un caso práctico de ingeniería eólica y, lo más importante, vamos a entender la física que hace que las palas giren.
El Caso de Estudio: Datos de la Instalación
Imagina una nave industrial que cuenta con una aeroturbina con las siguientes especificaciones:
- Radio de las palas (
): 4 metros. - Velocidad del viento (
): 22,22 m/s (¡un viento bastante fuerte!). - Densidad del aire (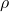): 0,928
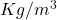(ajustada a la altitud de la explotación).
El objetivo: Calcular cuánta energía produce en una jornada de 10 horas.
El Secreto: ¿Por qué la velocidad es al cubo?
Mucha gente se sorprende al ver la fórmula de la potencia eólica. No es lineal, ni siquiera es al cuadrado… ¡es al cubo!
![\[P = \frac{1}{2} \cdot \rho \cdot A \cdot v^3\]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-3fc6157b9dd7f2ab98054d3474b3e30b_l3.png "Rendered by QuickLaTeX.com")
¿Por qué? Porque cuando el viento sopla más fuerte, ocurren dos cosas a la vez:
- Cada «paquete» de aire golpea con más energía cinética (relación al cuadrado).
- Pasan más paquetes de aire por segundo a través de las palas (relación lineal).Resultado:
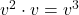. ¡Un pequeño aumento en la velocidad del viento dispara la producción!
Paso a Paso: El Cálculo
1. El Área de Barrido (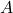
)
Las palas de 4 metros dibujan un círculo invisible en el aire. Ese es nuestro «captador»:
![\[A = \pi \cdot r^2 = \pi \cdot 4^2 \approx 50,27 \text{ m}^2\]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-69358a4fbfbba29befb6439d69ea8276_l3.png "Rendered by QuickLaTeX.com")
2. Potencia Instantánea (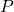
)
Aplicamos la fórmula con nuestros datos:
![\[P = 0,5 \cdot 0,928 \cdot 50,27 \cdot (22,22)^3\]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-0e55dd141f4addf8328cbe55e1219d11_l3.png "Rendered by QuickLaTeX.com")
![\[P \approx 255.866 \text{ W} \implies \mathbf{255,87 \text{ kW}}\]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-72f8a88117063faf183fd0bf820a2272_l3.png "Rendered by QuickLaTeX.com")
3. Energía Total en 10 Horas (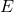
)
La energía es potencia por tiempo. Si el viento se mantiene constante:
![\[E = 255,87 \text{ kW} \cdot 10 \text{ h} = \mathbf{2.558,7 \text{ kWh}}\]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-83fc6b03757464db3e7f6aa874183728_l3.png "Rendered by QuickLaTeX.com")
Realidad vs. Teoría: El Límite de Betz
Aunque nuestro cálculo nos da 2.558,7 kWh, en la vida real no podemos extraer el 100% de esa energía. Si lo hiciéramos, el viento se detendría por completo tras las palas, ¡y el aire dejaría de fluir!
Existe un límite físico llamado Límite de Betz, que nos dice que solo podemos capturar, como máximo, el 59,3% de la energía del viento. Sumando las pérdidas mecánicas y eléctricas, una turbina real suele aprovechar entre el 30% y el 45%.
Conclusión
Calcular el potencial eólico es el primer paso para una gestión energética inteligente. Con los datos correctos, podemos prever si nuestra explotación será capaz de alimentar sus sistemas automatizados solo con la fuerza de la naturaleza.