PAU Andalucía Junio’25 – Ejercicio 2 – Opción A

a. Un motor Otto de 4T y 4 cilindros consume 9 litros a la hora de un combustible cuyo poder calorífico es 41000 kJ/kg y densidad 0.850 kg/l. Se sabe que tiene un rendimiento del 40 %, el diámetro de cada pistón es 70 mm y la carrera 90 mm. Obtener la potencia desarrollada y la cilindrada del motor.

b. Mediante una bomba de calor reversible se quiere climatizar una nave industrial a 23 ºC en invierno. La máquina tiene una eficienca real de 5 y se sabe que es el 30 % de la ideal. Calcular la temperatura media en el exterior.

a. El motor consume una masa de combustible de:

$9 \frac{l}{h}\cdot 0.850 \frac{kg}{l}=7.65 \frac{kg}{h}$

La energía consumida será:

$7.65 \frac{kg}{h}\cdot 41000\frac{kJ}{kg}=313650\frac{kJ}{h}$

Como el motor tiene un rendimientos del 40 %

$0.4\cdot313650\frac{kJ}{h} = 125460\frac{kJ}{h}$

Para calcular la potencia (energía/tiempo) realizamos la conversión de unidades:

$1W = \frac{1J}{1s}\Rightarrow P=\frac{125460\cdot 10^3 \frac{J}{h}}{3600 \frac{s}{h}}=34850W$

Para obtener la cilindrada del motor comenzamos por obtener el volumen de fluido que alberga un cilindro a partir de los datos geométricos facilitados

$V_{c}=S\cdot L=\frac{\pi\cdot d^2 }{4}\cdot L=$

$\frac{\pi \cdot {(70\cdot 10^{-3}m)}^2}{4} \cdot 90\cdot{10^{-3}}m=3.464\cdot{10^{-4}}\frac{m^3}{cil}$

Por lo que el volumen total del motor, que dispone de 4 cilindros será:

$V_{T} = 4\cdot V_{c} = 4 \cdot 3.464 \cdot 10^{-4}m^3 = 1.385 \cdot 10^{-3} m^{3}$

b. Con los datos proporcionados en el enunciado podemos dibujar un diagrama de funcionamiento de la bomba de calor

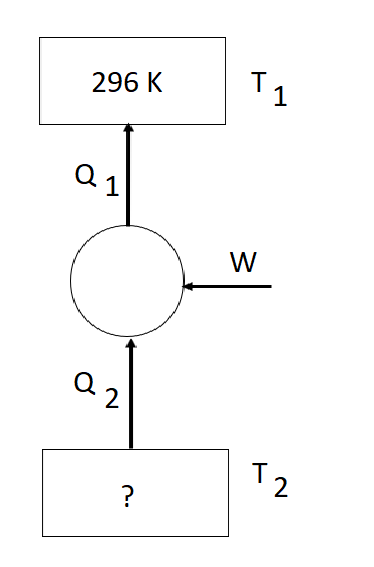
Nos dice que la eficiencia real de la máquina es el 30 % de la ideal.

$\epsilon ' = 0.3 \cdot \epsilon '_{Carnot}$

Por tanto:

$\epsilon'_C=\frac{\epsilon'}{0.3} \Rightarrow \epsilon'_C=\frac{5}{0.3}=16.67$

Y como la eficiencia de una máquina reversible que trabaje entre las mismas temperaturas es:

$\epsilon'_C=\frac{T_1}{T_1-T_2}$

Tenemos que:

$16.67=\frac{296 K}{296 K-T_2} \Rightarrow T_2= 278.24 K \Rightarrow T_2=5.24 ºC$

Post Relacionados

Deja un comentario Cancelar respuesta