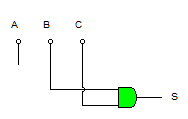
PAU Andalucía Junio’25 – Ejercicio 3 – Opción B

a. Dado el circuito siguiente, obtener otro que realice la misma función con puertas de dos entradas.

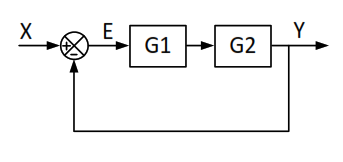
b. El sistema de control de lazo cerrado de la figura tiene un regulador con ganancia G1 y una planta con ganancia G2 = 50. Determinar el valor de G1 para que el error E sea inferior a 0.1 cuando la entrada X es igual a 1.

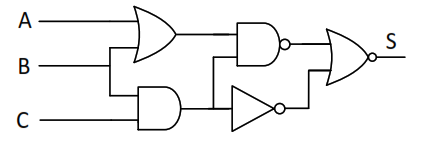
a. Vamos a obtener la función de salida del circuito y a simplificarla utilizando las leyes del Álgebra de Boole

En la salida de la puerta OR superior tenemos $A+B$

En la salida de la puerta AND inferior tenemos $BC$

En la salida de la puerta NAND superior tenemos $\overline{(A+B)BC}$

En la salida de la puerta NOT inferior tenemos $\overline{BC}$

Finalmente en la salida de la puerta NOR final tenemos $S=\overline{\overline{(A+B)BC}+\overline{BC}}$

Comenzamos quitando el paréntesis

$S=\overline{\overline{ABC+BC}+\overline{BC}}$

Aplicamos la Ley de Morgan al primer sumando

$S= \overline{\overline{ABC}\cdot \overline{BC}+\overline{BC}}$

Sacamos factor común $\overline{BC}$

$S= \overline{\overline{BC}(\overline{ABC}+1)}$

Como $\overline{ABC} + 1=1$ tenemos que:

$S= \overline{\overline{BC}\cdot 1}=\overline{\overline{BC}}=BC$

b. Vamos a escribir las funciones de error y de salida

La función de error a continuación del comparador será: $E=X-Y$

La función de salida, al estar los dos bloques en serie será: $Y=(G_1 \cdot G_2)\cdot E$

Se trata de un sistema de control con realimentación negativa, luego su función de transferencia es:

$\frac {Y}{X}=\frac{G_1 \cdot G_2}{1+G_1 \cdot G_2}$

Tenemos entonces que:

$Y=\frac{G_1 \cdot G_2}{1+G_1 \cdot G_2} \cdot X$

Luego sustituyendo en la expresión de la función de error $E=X-Y$ tenemos:

$E=X-\frac{G_1 \cdot G_2}{1+G_1 \cdot G_2} \cdot X =$

$=X \cdot \left({1-\frac{G_1 \cdot G_2}{1+G_1 \cdot G_2} \right) =$

$=X \cdot \frac{1+{G_1} \cdot {G_2}-G_1 \cdot G_2}{1+G_1 \cdot G_2} =$

$=X\cdot \frac{1}{1+G_1 \cdot G_2}$

Para que la señal de error sea menor de 0.1 y como X=1 y G2=50, tenemos que:

$0.1 > \frac{1}{1+50\cdot G_1}$

Trabajamos la expresión para obtener el valor de G1

$0.1 + 5\cdot G_1 > 1 \Rightarrow G_1 > \frac{0.9}{5} \Rightarrow G_1 > 0.18$

Post Relacionados

Deja un comentario Cancelar respuesta