La figura muestra un circuito lógico con tres entradas (A, B y C) y una salida S.
- Obtener la tabla de verdad y la expresión algebraica de la función lógica de salida S. (1 punto)
- Simplificar dicha función por el método de Karnaugh e implementarla con puertas lógicas de tipo NAND (1 punto)
- Convertir a decimal los siguientes números binarios: 0110, 1110, 0001, 1000 y 1111. (0.5 puntos)
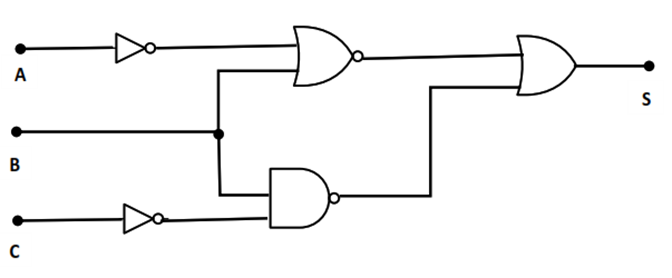
a. De la puerta NOT superior sale la señal ![]()
De la puerta NOT inferior sale la señal ![]()
De la puerta NOR superior sale la señal ![]()
De la puerta NAND inferior sale la señal ![]()
De la puerta OR final sale la señal ![]()
Cuya tabla de la verdad será:
| | S | ||||||
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
La expresión algebraica en 2ª forma canónica (maxterms) será:
![]()
b. Dibujamos el mapa de Karnaugh para tres variables.
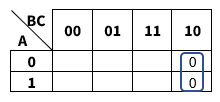
Que nos da la siguiente expresión simplificada:
![]()
Para implementarla con puertas lógicas de tipo NAND negamos dos veces y aplicamos las Leyes de De Morgan
![]()
Su implementación con puertas NAND será:
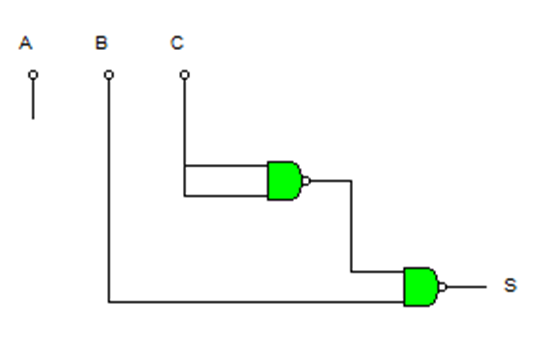
c. Podemos realizar la conversión utilizando potencias de 2, pero en este caso es sencillo, ya que son números de la primera quincena de decimales.
0110 – 6
1110 – 14
0001 – 1
1000 – 8 1111 – 15
1111 – 15
![]()
![]()
![]()
![]()
![]()

