Mediante un sistema acondicionador de aire se quiere climatizar un local y mantener la temperatura interior constante a 25ºC durante todo el año. La temperatura media del exterior es 10ºC en invierno y 35ªC en verano. La eficiencia de la máquina es el 35% de la ideal y la potencia del compresor es 4 kW. Calcular:
- La eficiencia de la máquina en invierno y en verano. (1 punto)
- El calor que extrae del local cada día en verano y el calor que cede al local cada día en invierno, suponiendo 5 horas de funcionamiento diario en ambos casos. (1.5 puntos).
a. En verano la máquina funciona como frigorífica, extrayendo calor del local y llevándolo al exterior:
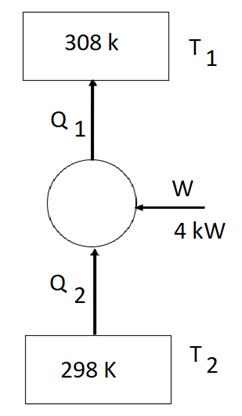
La eficiencia ideal de esta máquina funcionando como refrigeración es la que tendría una máquina de Carnot reversible que trabajase entre los dos mismos focos:
![\[ \epsilon_C = \frac{T_2}{T_1 - T_2} = \frac{298k}{308K - 298 K} = 29.8 \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-1acf69ffdfeabbab8ace196548b6f315_l3.png "Rendered by QuickLaTeX.com")
Como la real es el 35% de la ideal tenemos que en verano:
![\[\epsilon = 0.35 \cdot \epsilon_C = 0.35 \cdot 29.8 = 10.43 \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-0ef84d05cf196d7021da7c60462f1ec2_l3.png "Rendered by QuickLaTeX.com")
En invierno la máquina funciona como bomba de calor, extrayendo calor del exterior e introduciéndolo en el local.
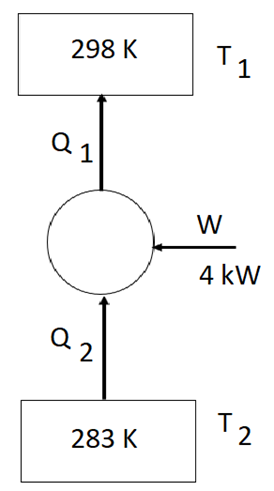
La eficiencia ideal de esta máquina sería la misma que la de una máquina de Carnot reversible trabajando entre las dos mismas temperaturas:
![\[\epsilon'_C = \frac{T_1}{T_1 - T_2} = \frac{298K}{298K - 283 K} = 19.87 \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-4930aae9aea4def202d5767022829398_l3.png "Rendered by QuickLaTeX.com")
La real será el 35% de la ideal:
![\[\epsilon' = 0.35 \cdot \epsilon'_C = 0.35 \cdot 19.87 = 6.95 \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-b74563224fb247ad1252583cc1f835ab_l3.png "Rendered by QuickLaTeX.com")
b. Para poder determinar las cantidades de calor absorbidas o cedidas en cada caso, primero calculamos la energía consumida por el compresor al día.
![\[ P= \frac{W}{t} \Rightarrow W = P \cdot t \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-b842aeabd67ddd1fd0b23a6800ddc879_l3.png "Rendered by QuickLaTeX.com")
![\[W = 4000 \frac{J}{s} \cdot {5 \frac{h}{día}} \cdot \frac{3600 s}{h} = 72 \cdot 10^6 \frac{J}{día} \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-a5b9c53e1c254f4d75dcc547678ad99f_l3.png "Rendered by QuickLaTeX.com")
En verano:
![\[ \epsilon = \frac{Q2}{W} \Rightarrow Q_2 = \epsilon \cdot W = 10.43 \cdot 72 \cdot 10^6 \thinspace {\frac{J}{día}} = 750960000 \frac{J}{día} \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-984e0f95ae62fcad3f78e6e0f5fd7bec_l3.png "Rendered by QuickLaTeX.com")
En invierno:
![\[ \epsilon'_C = \frac{Q_1}{W} \Rightarrow Q_1 = \epsilon'_C \cdot W = 6.95 \cdot 72 \cdot 10^6 { \frac{J}{día}} = 500400000 \frac{J}{día} \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-eaaa551c09dc5a5274d2464fef920983_l3.png "Rendered by QuickLaTeX.com")