a. En una habitación se utiliza un sistema automatizado para controlar las luces, F, en función de las tres entradas siguientes:
- Sensor de movimiento M (hay personas en la habitación =”1”, no hay personas =”0”).
- Sensor de luz ambiente L (luz insuficiente =”1”, luz adecuada =”0”).
- Interruptor manual S (encendido manual =”1”, encendido automático =”0”)
Las luces, F, se encenderán en algunos de los siguientes casos: i) se detecta movimiento y la luz ambiente es insuficiente; ii) el interruptor manual está activado independientemente del resto de condiciones. Se pide:
a.1. Obtener la tabla de la verdad para F y su función en forma canónica. (0.75 puntos)
a.2. Simplificar por el método de Karnaugh e implementar la función con puertas NAND. (1 punto)
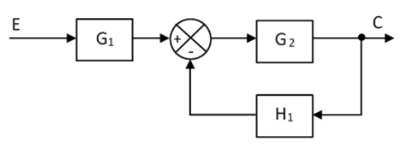
b. Obtener la función de transferencia C/E del siguiente sistema de control. (0.75 puntos)
La tabla de la verdad que cumple las condiciones del enunciado es:
| M | L | S | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
La función en forma canónica (1ª canónica o minterms) es la siguiente:
![]()
a.2. Dibujamos el mapa de Karnaugh para tres variables.
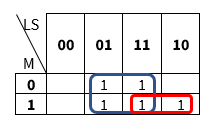
Obtenemos la función:
![]()
Para implementarla con puertas NAND negamos dos veces para que no varíe la función y aplicamos la Leyes de Morgan:
![]()
Ya podemos realizar la implementación con puertas NAND:
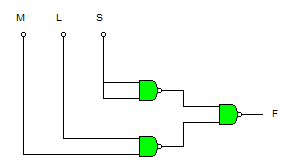
b. Para obtener la función de transferencia, escribimos las ecuaciones de las señales en cada uno de los puntos del sistema de control en los que la señal cambia de valor.
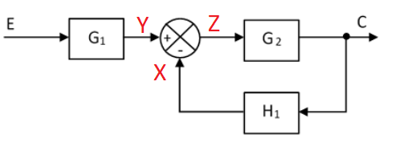
![]()
![]()
![]()
![]()
Operamos con las ecuaciones de las señales:
![]()
![]()
![]()
Agrupando tenemos que:
![]()
Finalmente:
![]()

