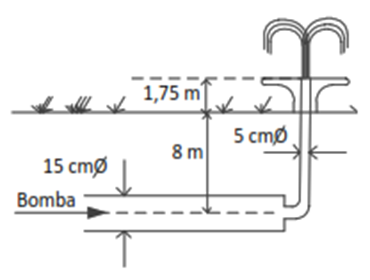
Se desea diseñar una fuente de agua para un hotel. Esta fuente estará alimentada por una tubería cilíndrica de 15 cm de diámetro situada horizontalmente a una profundidad de 8m bajo el nivel del suelo. Posteriormente, la tubería se conectará a otra tubería cilíndrica de 5 cm de diámetro que se curvará hacia arriba y el agua será expulsada por el extremo de esta. Dicho extremo estará a una altura de 1.75 m por encima del suelo y el agua se proyectará con una velocidad de 12 m/s.
Dato: densidad agua = 1000 kg/m3.
- Calcular el caudal de agua cuando está en funcionamiento (1 punto).
- Calcular la presión manométrica necesaria en la tubería horizontal (1 punto).
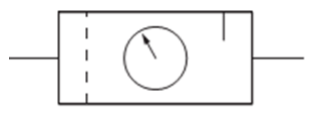
- Representar el símbolo de la unidad de mantenimiento en una instalación neumática y citar sus componentes (0.5 puntos)
a. Para poder calcular el caudal de agua aplicaremos:
![]()
![]()
![]()
b. Para calcular la presión manométrica en la tubería horizontal aplicamos la expresión de Bernoulli entre el punto que está a 8 m de profundidad y en la salida del agua en la fuente, a 1.75 m por encima de la superficie.
![]()
![]()
Donde:
- p2 = 0. Ya que es la presión manométrica a la salida de la fuente.
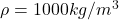
- g = 9.8 m/s2
- v2 = 12 m/s
- Para calcular v1 utilizamos la ecuación de continuidad.
![]()
![Rendered by QuickLaTeX.com \[v_1 = \frac{S_2}{S_1} \cdot v_2 = \frac{\frac{\pi \cdot d_2^2}{4}}{\frac{\pi \cdot d_1^2}{4}} \cdot v_2 = \frac{d_2^2}{d_1^2} \cdot v_2 = \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-bc137ebec967058ab06ae7f7435fbe90_l3.png)
![]()
- h1 = -8 m (está por debajo del suelo)
- h2 = 1.75 m (está por encima del suelo)
![]()
![]()
![]()
c. La unidad de mantenimiento de una instalación neumática está compuesta por un filtro, un regulador de presión y un lubricador. El filtro elimina las partículas que puede llevar el aire, el regulador mantiene la presión a un nivel constante en la instalación y el lubricador pulveriza aceite en el aire que sirve para evitar desgaste y oxidación en la instalación neumática. Su símbolo normalizado es el siguiente: