Dado el circuito lógico de la figura:
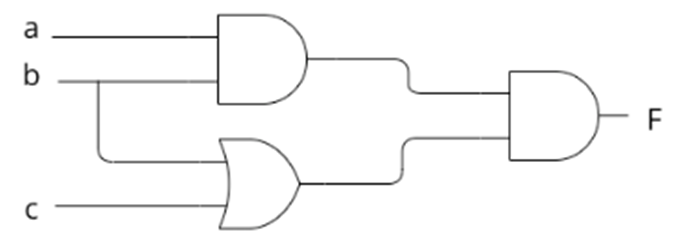
- Obtener la tabla de la verdad y expresar la función lógica F en su forma canónica (1 punto)
- Simplificar la función F mediante el método de Karnaugh e implementarla con puertas lógicas (1 punto).
- Determinar qué números binarios representan los siguientes números decimales: 14, 27, 45, 28 y 36 (0.5 puntos)
a. Para obtener la tabla de la verdad primero obtenemos la función lógica a través del circuito lógico.
- De la puerta AND superior obtenemos:
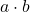
- De la puerta OR inferior obenemos:
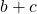
- De la puerta AND de la derecha obtenemos finalmente:
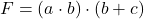
Para obtener la forma canónica en primer lugar desarrollamos la función quitando paréntesis.
![]()
Para tener la primera forma canónica o minterms nos falta en el primer sumando la variable c. Para conseguirla multiplicamos el primer sumando por ![]() , que al ser 1 no modifica la expresión.
, que al ser 1 no modifica la expresión.
![]()
Desarrollamos la expresión:
![]()
Y ya tenemos la forma canónica.
Procedemos a construir ahora la tabla de la verdad de la función.
| a | b | c | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
b. Dibujamos el mapa de Karnaugh para tres variables para la función F
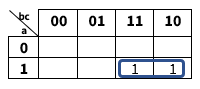
Luego la función simplificada quedaría así:
![]()
Cuya implementación con puertas lógicas es la siguiente:
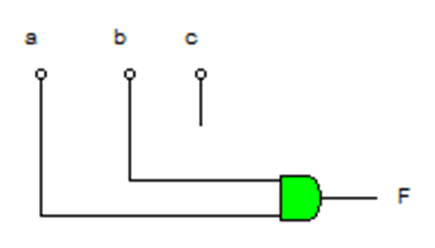
c. Para obtener los binarios correspondientes a los decimales dados debemos dividir por dos hasta que el cociente sea 0 y tomar los restos de las divisiones desde el último al primero
14:2 = 7 | 0
7:2 = 3 | 1
3:2 = 1 | 1
1:2 = 0 | 1 1410 = 11102
27:2 = 13 | 1
13:2 = 6 | 1
6 :2 = 3 | 0
3 :2 =1 | 1
1:2 = 0 | 1 2710 = 110112
45:2 = 22 | 1
22:2 = 11 | 0
11:2=5 | 1
5:2 = 2 |1
2:2 = 1 | 0
1:2 = 0 |1 4510 = 1011012
28:2 =14 | 0
14:2=7 | 0
7:2=3 | 1
3:2=1 | 1
1:2=0 | 1 282 = 111002
36:2=18 | 0
18:2=9 | 0
9:2=4 | 1
4:2=2 | 0
2:2=1 | 0
1:2=0 | 1 362 = 1001002

