PAU Andalucía Titular A Junio’24 – Ejercicio 4

De un motor Diésel de cuatro cilindros y cuatro tiempos se sabe que el diámetro de sus cilindros es 60 mm, la carrera 90 mm y la relación volumétrica de compresión 20:1. El motor desarrolla un par de 53 Nm para una potencia de 20 kW.

Calcular el volumen de la cámara de combustión y la cilindrada del motor. (1 punto).
Calcular el régimen de giro en rpm cuando se desarrolla un par motor de 53 Nm (1 punto).
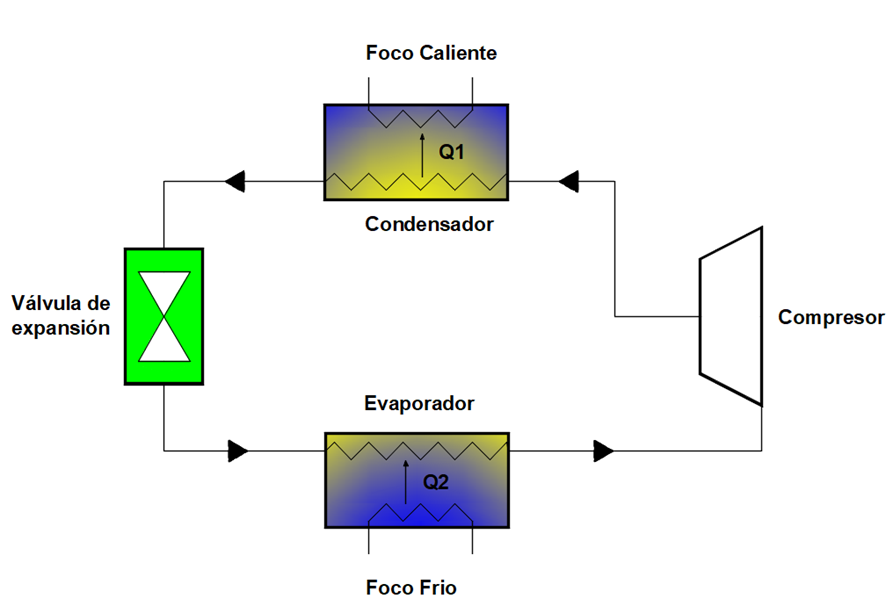
Representar el esquema de una máquina frigorífica indicada sobre este los elementos fundamentales que la componen (0.5 puntos).

Para calcular la cilindrada del motor, primero calcularemos el volumen de un cilindro a partir de las características geométricas del enunciado.

$V_u = S \cdot L = \frac{\pi \cdot d^2}{4} \cdot L = \frac{\pi \cdot (6 cm)^2}{4} \cdot 9 cm = 254.47 cm^3$

Como el motor tiene cuatro cilindros, la cilindrada total será:

$V_T = V_u \cdot 4 = 254.47 cm^3 \cdot 4 = 1017.88 cm^3$

El volumen de la cámara de combustión lo podemos obtener a través de la relación volumétrica de compresión:

$R_c = \frac{V_u + V_c}{V_c} \Rightarrow V_c = \frac{V_u}{R_c-1} = \frac{254.47 cm^3}{20-1} = 13.39 cm^3$

b. Para calcular el régimen de giro utilizamos la expresión que relaciona la potencia, el par y el régimen de giro:

$P = M \cdot \omega$

Despejando la velocidad angular y convirtiendo el resultado a rpm tenemos que:

$\omega = \frac{P}{M} = \frac{20 \cdot 10^3 W}{53Nm} = 377.36 \frac{rad}{s}$

$\omega = 377.36 \frac{rad}{s} \cdot \frac{1 \thinspace rev}{2 \cdot \pi \thinspace radianes} \cdot \frac{1min}{60 s}= 3603.5 rpm$

c. El esquema de una máquina frigorífica con sus elementos fundamentales podría ser el siguiente:

Post Relacionados

Deja un comentario Cancelar respuesta