En un ensayo Brinell de dureza se aplica una carga de 250 kp con un penetrador de 5 mm de diámetro. Tras un tiempo de aplicación de 15 s, se genera una huella de 2 mm de diámetro.
- Obtener la dureza de Brinell y su expresión normalizada. (1 punto).
- Si se cambia el penetrador por uno de 10 mm de diámetro, calcular la carga aplicada y el diámetro de la huella para obtener el mismo valor de dureza. (1 punto).
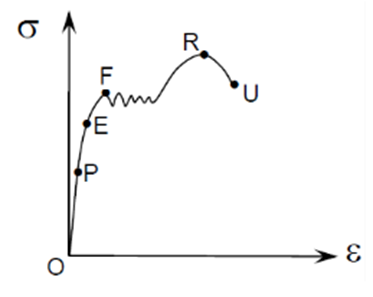
- La figura muestra un diagrama del ensayo de tracción de un material. Indicar qué nombre se les da a los puntos P, E, F, R y U y su significado. (0.5 puntos).
a. La dureza Brinell se calcula relacionando la fuerza aplicada en el ensayo con la superficie de la huella que deja el penetrador a través de la siguiente expresión matemática:
![\[ HB = \frac{2 \cdot F}{\pi \cdot D \cdot (D - \sqrt{(D^2-d^2)}} = \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-e65970957feb6b1c10efee25c4f2d35c_l3.png "Rendered by QuickLaTeX.com")
![\[ HB = \frac{2 \cdot 250kp}{\pi \cdot 5mm \cdot (5mm - \sqrt{((5mm)^2-(2mm)^2)}} = 76.26 \frac{kp}{mm^2} \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-8669ecd28045d41807b08b5e7fdc957c_l3.png "Rendered by QuickLaTeX.com")
La expresión normalizada incluye el valor de la dureza, el penetrador usado, la fuerza aplicada el tiempo de aplicación:
76.26 HB 5 250 15
b. Para que los dos ensayos sean equivalentes, deben tener la misma constante.
La constante del primer ensayo es:
![\[ F_1 = k \cdot D_1^2 \Rightarrow k=\frac{F_1}{D_1^2} = \frac{250kp}{(5mm)^2} = 10 \frac{kp}{mm^2} \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-3340d57223d35302f620b8a69aec53ca_l3.png "Rendered by QuickLaTeX.com")
El diámetro de la nueva huella, despejando de la expresión de la dureza Brinell será:
![\[ d = \sqrt{ \frac{4F}{HB \cdot \pi} - \left( \frac{2F}{HB \cdot \pi D} \right)^2 }= \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-9c58ece29af32f9e7853389393d49cab_l3.png "Rendered by QuickLaTeX.com")
![\[ d = \sqrt{ \frac{4 \cdot 1000kp}{76.26kp/mm^2 \cdot \pi} - \left( \frac{2 \cdot 1000 kp}{76.26 kp/mm^2 \cdot \pi \cdot 10mm} \right)^2 }= 4 mm \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-77f2b5162db89a669d9a08270fd42a9e_l3.png "Rendered by QuickLaTeX.com")
También se puede calcular con una simple proporción entre los diámetros:
![\[ \frac{d_2}{D_2} = \frac{d_1}{D_1} \Rightarrow d_2 = d_1 \cdot \frac{D_2}{D_1} \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-33fb8d8128d8a21c0903430927411ece_l3.png "Rendered by QuickLaTeX.com")
![\[ d_2 = 2 mm \cdot \frac{10mm}{5mm}= 4mm \]](https://technoteacher.es/wp-content/ql-cache/quicklatex.com-7df479a718ec450adfe628263b887394_l3.png "Rendered by QuickLaTeX.com")
c. El diagrama mostrado es un diagrama tensión-deformación para un material en un ensayo de tracción, que presenta los siguientes puntos característicos:
- Punto P. Es el límite de proporcionalidad. Este punto marca el límite de deformaciones elásticas en el que las deformaciones son proporcionales a la tensión aplicada, es decir, cumplen la Ley de Hooke.
- Punto E. Es el límite elástico. A partir de esta tensión las deformaciones del material son permanentes.
- Punto F. Es el límite de fluencia. A partir de este punto el material se deforma plásticamente si apenas incremento de la tensión aplicada.
- Punto R. Resistencia a la tracción. Es la máxima tensión que el material soporta. A partir de aquí, el material se sigue deformando, se produce la estricción y la tensión disminuye hasta la rotura de la probeta.
- Punto U. Es el punto de fractura, donde finalmente la probeta se rompe.